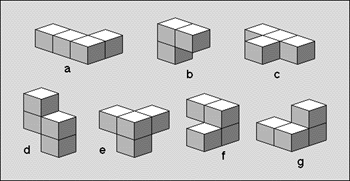
Figure: The seven pieces that once formed a cube
| Cube |
There was once a 3 by 3 by 3 cube built of 27 smaller cubes. It has fallen apart into seven pieces:

Figure: The seven pieces that once formed a cube
The seven pieces can be assembled in many ways to again form the cube. Figure 2 shows one of these possibilities. The first square stands for the front plane, the next one for the middle plane and the last one for the back plane of the cube. The letters in the cells stand for the name of piece filling out the corresponding space in the cube. The name of the seven pieces can be found in figure 1.
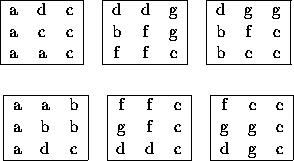
Figure: Two possibilities of assembling the cube
You are to write a program that outputs all possibilities of assembling the cube but suppress solutions that are mere rotations of another solution. The time limit for this problem is 15 minutes!
Hint: Piece a is the only part that, by rotation and translation, cannot be transformed into itself. In order to avoid solutions that are mere rotations of an already found solution, you may restrict transformations of piece a to translations.
No input is needed.
For each solution found, your program should output a line containing the solution as a string. The string is a linearized form of the cube. Each letter stands for the piece filling out the corresponding space in the cube. It is linearized as follows:
adcaccaacddgbfgffedggbfebee aababbadcffegfcddcfeeggedgc
It is very important that your program uses the naming convention given in figure 1 and linearizes the cube as explained above.
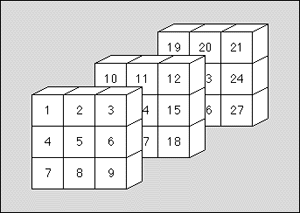
Figure: Positions of the cells in the string
Figure 3 again shows how the cells of the cube are linearized.
The output of your program could start like this:
aababbadcggeffcddcgeegfedfc aababbadceffgdcgdceefedfggc aababbadcffegfcddcfeeggedgc ...