Применение преобразования Фурье в цифровой обработке звука

В данной статье описывается дискретное преобразование Фурье применительно к теории цифровой обработки звука, его свойства и алгоритм возможной реализации. Все математические выкладки приведены без доказательств, которые могут быть найдены в соответствующих пособиях по математическому анализу.

Общие сведения

Как известно, звуковой сигнал в компьютере может представляться в виде некоторого набора отсчётов его амплитуд, производимых через определённые промежутки времени (период дискретизации) и представляемых некоторым количеством двоичных разрядов (разрядность выборки). Такое представление удобно для хранения звукового сигнала и его преобразования обратно в непрерывный сигнал. Однако, некоторые операции обработки звукового сигнала в таком представлении бывает не всегда удобной. Это связано с тем, что реально звуковой сигнал складывается из составляющих его частот с определённой амплитудой и фазой. Таким образом, применение таких операций обработки звукового сигнала как "фильтр нижних частот" или "фильтр верхних частот" требует преобразования представления звукового сигнала в виде отсчётов в его частотный спектр. После этого преобразования звуковой сигнал будет представлен в виде коэффициентов, соответствующим амплитудам и фазам частот, составляющих этот сигнал. Теперь, например, операция "фильтр нижних частот", которая "вырезает" из сигнала все частоты выше некоторой заданной, может просто обнулить коэффициенты, соответствующие частотам, которые необходимо "вырезать". На самом деле, круг областей применения такого преобразования значительно шире: обработка растровых изображений, телекоммуникации, исследование и измерение сигналов, радиолокация и т.д. Примером применения преобразования может служить передача данных в цифровой форме по аналоговым линиям телефонной сети (модем). Для передачи данных в цифровой форме, они сначала преобразуются в некоторый набор частот и передаются по линиям передач, а затем, на приёмной стороне выполняется обратное преобразование и восстанавливаются исходные данные. Далее рассмотрены некоторые фундаментальные понятия из математического анализа, необходимые для понимания работы преобразования Фурье.

Ряд Фурье

Рядом фурье называется бесконечная математическая последовательность, состоящая из коэффициентов при функциях синуса и косинуса вида:

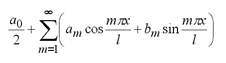
Доказано, что если некоторая периодическая функция с периодом 2l на интервале [-l, l] удовлетворяет условиям Дирихле (непрерывна и имеет конечное число экстремумов и точек разрыва I рода), то она может быть представлена в виде суммы ряда Фурье (разложена в ряд Фурье). Для определения коэффициентов ряда Фурье справедливы следующие формулы:

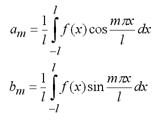
Если раскладываемая функция является чётной ( f(-x) = f(x) ), то ряд Фурье состоит только из косинусов, т. е. все коэффициенты при синусах равны 0. Если раскладываемая функция является нечётной ( f(-x) = -f(x) ), то ряд Фурье состоит только из синусов, т. е. все коэффициенты при косинусах равны 0. В общем случае, коэффициенты при синусах и косинусах не равны 0.

Таким образом, любую периодическую функцию, удовлетворяющую условиям Дирихле, можно разложить в ряд Фурье, тем самым представляя её в виде суммы синусов и косинусов.

Преобразование Фурье в общем виде

Предположим теперь, что исследуемая функция не является периодической, т. е. её период повторения равен бесконечности. В этом случае справедлива интегральная формула Фурье, получаемая путём предельного перехода из ряда Фурье периодической функции с периодом 2l при l ® ?:

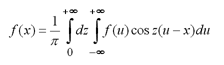
С этой формулой связаны так называемые интегральные преобразования Фурье:

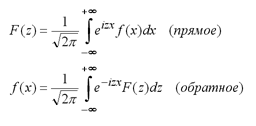
Из этих формул можно вывести синус- и косинус-преобразования Фурье соответственно для нечётных и чётных функций. Синус-преобразование Фурье:

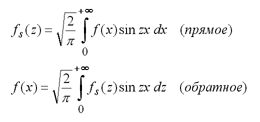
Косинус-преобразование Фурье:

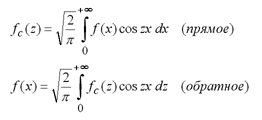
Таким образом, непрерывное преобразование Фурье позволяет представить непериодическую функцию в виде интеграла функции, представляющей в каждой своей точке коэффициент ряда Фурье для непериодической функции.

Метод корреляций

Метод корреляций позволяет определить тесноту линейной зависимости между исследуемой и базисной функциями. Это легче понять на примере. Пусть имеется импульсная радиолокационная станция. Для обнаружения цели эта станция формирует короткий высокочастотный радиоимпульс, огибающая которого имеет прямоугольную форму. Этот импульс излучается в пространство и отражается от цели. Так как в однородной среде электромагнитные волны распространяются с постоянной скоростью, близкой к скорости света в вакууме, то зная время, через которое отражённый от цели импульс поступил в приёмник радиолокационной станции, можно определить расстояние до цели. Однако здесь возникает следующая проблема: так как только часть импульса отражается от цели и поступает обратно в приёмник, а также в приёмник поступают некоторые помехи и сам приёмник имеет некоторый коэффициент шума, результирующий импульс будет несколько размыт на фоне помех и шумов. Возникает вопрос, как определить какая часть графика, представленного на рис. будет представлять отражённый импульс? Воспользуемся следующим методом: возьмём за основу функцию, которая на некотором интервале будет иметь скачок, представляющий собой идеальный отражённый импульс (при отсутствии помех и ослаблений) . Далее будем в каждой точке перемножать эту базисную функцию на функцию, формируемую приёмником, а затем проинтегрируем полученную функцию. Таким образом, это преобразование позволяет определить насколько велико значение базисной функции в исследуемой. Если исследуемая функция в каждой своей точке равна базисной, то интеграл функции, полученной в результате этого преобразования будет иметь максимальное значение. Если исследуемая функция ни как не отражает базисную, то результат будет равен 0. В промежуточных вариантах значения интеграла результирующей функции будут отражать то, насколько точно исследуемая функция соответствует базисной. Это и есть метод корреляций. Вернёмся к определению расстояния до цели. Теперь будем формировать новую базисную функцию, интервал скачка которой будем смещать вправо по оси абсцисс. Как только этот интервал будет соответствовать интервалу функции, соответствующему отражённому импульсу, значение интеграла результирующей функции будет максимальным. Таким образом может решаться задача об определении расстояния до цели.

Дискретное преобразование Фурье

В дискретном преобразовании Фурье исследуемая функция является периодической имеет конечный период повторения, и является дискретной. Фактически, дискретное преобразование Фурье позволяет представить дискретную функцию в виде конечного числа частот с определёнными значениями амплитуды и фазы (раскладывает функцию в её спектр). Это основывается на том, что по следствию из теоремы Котельникова в дискретном сигнале период, соответствующий наивысшей представимой частоте соответствует двум периодам дискретизации. Для определения амплитуд и фаз частотных составляющих сигнала, в дискретном преобразовании Фурье используется корреляция с базисными функциями синуса и косинуса. Спектр частот в дискретном преобразовании Фурье определяется из амплитуд синусов и косинусов, с частотами повторения в исследуемой выборке от 0 до N/2 раз, где N - количество элементов выборки. Преобразование Фурье раскладывает дискретизированный сигнал из N выборок на N/2 + 1 синусных и N/2 + 1 косинусных составляющих. Почему именно синусных и косинусных? Не только потому, что это следует из формулы ряда Фурье. Установлено, что результат сложения двух взаимно перпендикулярных колебаний с одинаковыми частотами, но разными амплитудами даёт колебание с той же частотой, но с другой амплитудой и фазой. Поэтому можно сказать, что дискретное преобразование Фурье раскладывает исследуемый сигнал по базисным функциям синуса и косинуса. Они являются аналогами двух взаимно перпендикулярных колебаний, так как по фазе смещены друг относительно друга на 90 градусов. Все вышеприведённые размышления приводят к следующим формулам дискретного преобразования Фурье:

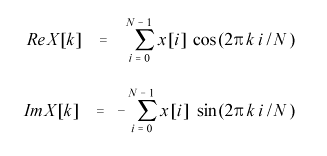
Эти формулы описывают прямое преобразование Фурье. ReX[x] - массив, содержащий значения косинусоидальных составляющих. ImX[x] - массив, содержащий значения синусоидальных составляющих. Такие обозначения введены в силу комплексного представления непрерывного преобразования Фурье (см. выше). При этом действительной части соответствуют косинусы, а мнимой - синусы. Это не должно вводить Вас в заблуждение - элементы этих массивов являются действительными числами и коэффициенты при синусах и косинусах являются действительными числами. Также, исследуемая функция является функцией действительного переменного. Комплексная форма преобразования Фурье может вводится для удобства записи двух интегралов - для косинуса и синуса. Массивы Re[x] и Im[x] составляют так называемый частотный домен (frequency domain), в то время как исходная выборка называется временным доменом (time domain).

Свойства дискретного преобразования Фурье

По приведённым выше формулам производится разложение исследуемого сигнала в его спектр. Выясним теперь свойства преобразования Фурье. Допустим, требуется произвести обратное преобразование - из частотных составляющих сформировать исходный сигнал. Для этого справедливы приведённые ниже формулы:

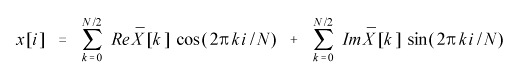
Коэффициенты ReX[k] и ImX[k] определяются по следующим формулам:

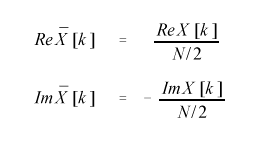
За исключением двух случаев:

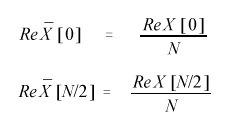
Такой процесс преобразования называется синтезом или обратным преобразованием Фурье. Заметим, что формулы обратного преобразования аналогичны формулам прямого преобразования, только теперь подынтегральной функцией являются коэффициенты при синусах и косинусах. Это свойство является очень важным и называется двойственностью преобразования Фурье. Свойство двойственности позволяет объяснить следующий факт: единичный импульс во временном домене (единичное значение одной выборки при нулевых значениях остальных) соответствует синусоиде и косинусоиде в частотном домене и наоборот (рис.). Во втором случае всё понятно - имеется один коэффициент при синусе или косинусе - это значит, что исходный сигнал (выборка) содержит составляющую одной частоты синусоидальной или косинусоидальной формы. Первый же случай может быть объяснён на основе двойственности преобразования Фурье. Описанный факт используется при построении алгоритма быстрого преобразования Фурье. Дело в том, что приведённые выше формулы для прямого и обратного преобразований имеют временную сложности реализующих их алгоритмов порядка O(n^2). Таким образом, при больших объёмах выборки, не удаётся за реальное время произвести преобразование Фурье. Для этой цели в середине 60-х годов был разработан алгоритм быстрого преобразования Фурье, который описывается в конце статьи.

Свойства амплитуды и фазы

Как уже было сказано, дискретное преобразование Фурье раскладывает исследуемый сигнал (выборку) на синусоидальные и косинусоидальные составляющие. В то же время, хотелось бы получить значения амплитуд и фаз частотных составляющих сигнала. Для перевода пары соответствующих коэффициентов при синусе и косинусе в амплитуду и фазу частотной составляющей справедливы следующие формулы:

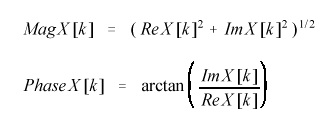
Обратное преобразование имеет вид:

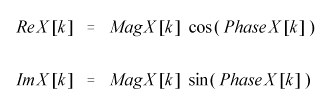
Полученные значения амплитуды и фазы называют полярным представлением (polar notation). Значения же коэффициентов при синусах и косинусах характеризуют прямоугольное представление (rectangular notation). При выполнении первого преобразования возможно несколько вариантов. 1. Значение коэффициента при косинусе равно 0. Тогда значение фазы равно ±p/2. Соответствующее значение выбирается в соответствии со знаком коэффициента при синусе - если он положительный, то значение фазы p/2, если отрицательный, то -p/2. 2. Значение коэффициента при синусе равно 0. Тогда значение фазы равно 0 или p. Соответствующее значение выбирается в соответствии со знаком коэффициента при косинусе - если он положительный, то значение фазы 0, если отрицательный, то p. 3. "Дрейф" фазы. Подобный эффект наблюдается при очень малом, близком к 0, значении коэффициента при косинусе. При этом возможны резкие скачки значений фазы от -p/2 к +p/2. Так как значения коэффициента при косинусе очень малы, то, практически, фаза в этом случае не имеет значения и её можно принять равной -p/2 или +p/2.

Как правило, значение фазы сигнала несёт в себе больше информации о форме и изменениях сигнала. Пусть, например, во временном домене имеется импульс некоторой длительности. Преобразуем этот временной домен в частотный и далее в полярное представление. Установим все амплитуды в случайное значение и преобразуем частотный домен обратно во временной. Таким образом, новый временной домен содержит в себе информацию, полученную из значений фаз частотных составляющих. Теперь в том месте, где был расположен импульс на его границах заметны скачки. Это и объясняет то, что фаза сигнала несёт больше информации о форме сигнала.

Эффект Гиббса. Предположим, что из спектра прямоугольного импульса, убрали все частоты выше некоторой заданной. Далее применили обратное преобразование Фурье. Теперь на границах импульса будут отчётливо заметны затухающие колебания. Это объясняется тем, что границы идеального импульса представляются бесконечным числом синусоид и косинусоид. При увеличении этого количества от 0 до бесконечности форма фронтов импульса принимает свой истинный вид. При меньшем же количестве синусоид и косинусоид на границах импульса появляются искажения. Этот эффект носит название эффекта Гиббса. Таким образом, применение цифровых фильтров, построенных на основе преобразования Фурье в некоторых случаях может искажать сигнал. Этим ограничивается область применения таких фильтров.

Алгоритм дискретного преобразования Фурье

Ниже представлен исходный текст программы на C++, реализующей алгоритм преобразования Фурье. Мнимая функция GetValues() записывает во временной домен (массив f) некоторые значения, определяющие исследуемый сигнал.

Быстрое преобразование Фурье

Как было отмечено выше, обычное дискретное преобразование Фурье имеет большую временну сложность алгоритма (порядка O(n^2)), что ограничивает его применение. Алгоритм быстрого преобразования Фурье основывается на таком математическом преобразовании как свёртка функций. Свёртка функций подробно описывается в учебниках по мат. анализу и здесь не рассматривается. Остановимся на некоторых характерных чертах работы алгоритма быстрого преобразования Фурье. Количество элементов в выборке, поступающих на вход быстрого преобразования Фурье должно быть 2^n. Временная сложность преобразования - O(n · log n). Алгоритм быстрого комплексного преобразования Фурье работает следующим образом.

Существуют модификации алгоритма для сигнала, выборки которого являются действительными числами. Для полного понимания работы этого алгоритма следует ознакомиться с теорией линейных систем, свёрткой, свойствами и парами преобразований Фурье и модификациями преобразований Фурье для функций комплексного переменного.